Our Night Sky
I was briefly able to see some stars in the night sky from flat in densely populated Kent. It made me miss the days of seeing a sky full of starts from my home in rural New Brunswick, Canada. No light would imped their brightness and on a clear evening everything would glow with a warm celestial, almost magically light. But since I am in lovely England, we will make do.
I started thinking about stars and constellations,and when it comes down to it, starts aligned in to constellations are just a series of points and lines connected to one another to which we humans ascribe meaning. You know what else is a series of lines and points? Scatter plots!
Research
So as usual we start with research and I found an excellent article by Kim Fitter who plotted a really complete map of the night sky and milky way. But I just want to see the stars, so what can we learn from Kim.
Well, she kindly has a series of data we can use.
stars_url <- "https://raw.githubusercontent.com/ofrohn/d3-celestial/master/data/constellations.lines.json"So now we go about the business of truing a JSON object into a series of constellations as defined as points and lines. However, now comes the head ache… projection.
The earth is round and so is the sky?
I made it sound like I am bored, but I am actually very excited! You see an ancient problem that still haunts us today is projection. The idea of how you wrap a 2D plane around a 3D globe so that the real size and shape of a geographical feature is not distorted. Imagine trying to wrap a basketball as a holiday present. Yeah, that bad. But it all depends on your point of view, literally. Here is the graph on a basic plane.

Projections are typically defined as Coordinate Reference Systems (CRS) and many exist. The first thing we need to figure out is what projection ‘shape’ we want. You can learn more here, but in brief we have three types.
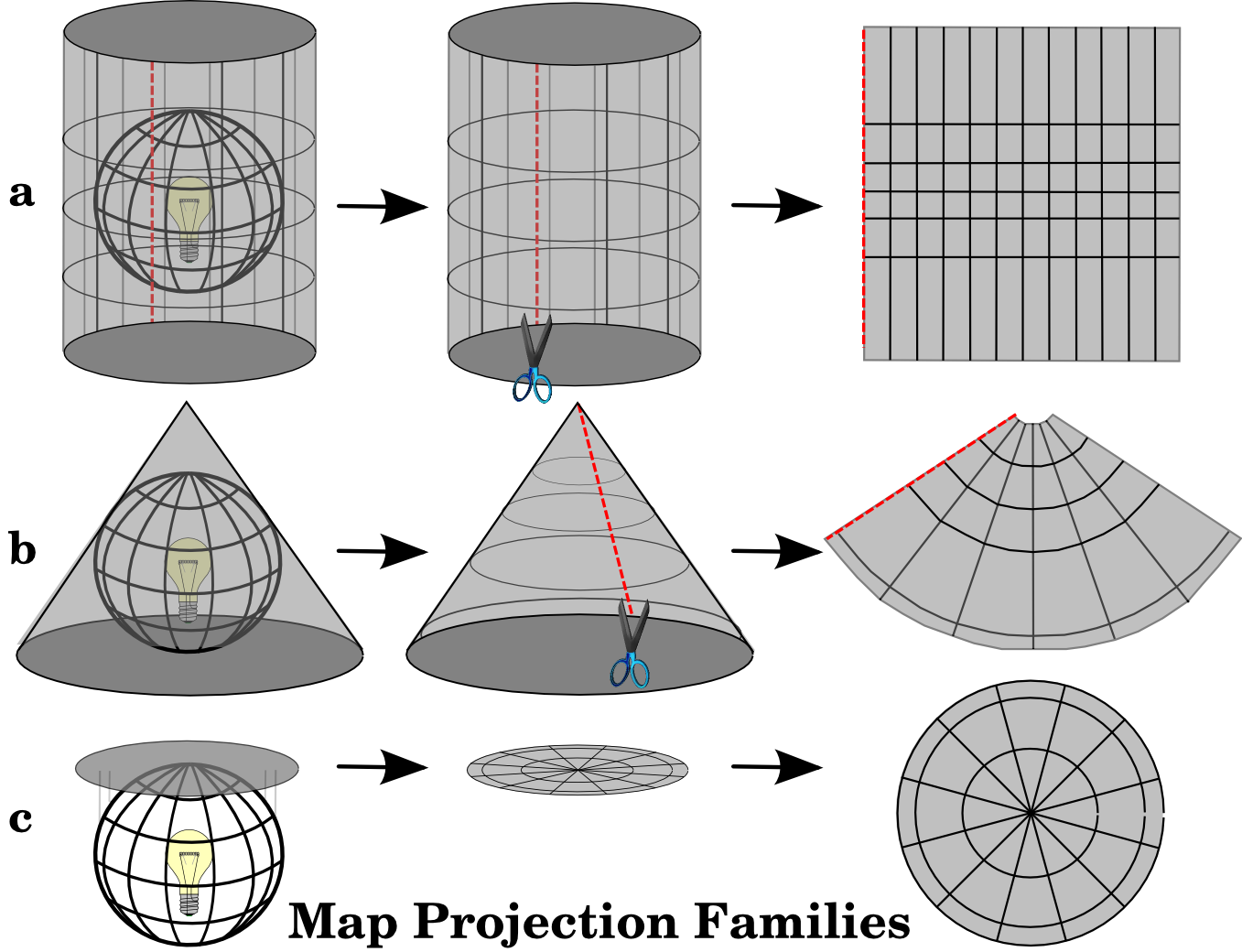
As you can see, none fit the round shape of a globe quite the way we would expect, or well. But now lets see how it distorts an actual world map.

Fun right? So which do you choose? And which do you choose when you are looking at the night sky? Well, Kim Fitter makes a few suggestions with the Mollweide (pronounced Moll-vi-de) appears to be a good approximation. As you can see it looks like a squashed circle. Mollweide attempts to strike a balance between shape and proportion, which accounts for a great deal of distortion for the sky when looking upwards as well as down wards. This simplifies the transformation so you don’t have to account for any complicated leaps or jumps at the edges of other transformations, points simply expand as the reach the equator and contract at the poles. So lets try it.

But lets add some labels so we can identify the the constellation

But I just want something simple, clean and satisfying. So why not force the shape to be round.

Et Voilà! So satisfying!